HVAC Systems
Flow of air in ducts
For this topic we will stay within the inch-pound system.
| Variable | Name | units |
|---|---|---|
| Q | Volume flow rate | $\ft^3/\min\equiv\cfm$ |
| v | Velocity | $\ft/\min\equiv\fpm$ |
| p | Pressure | $\inWC$ |
Friction losses in straight runs
Air flows at 6000 cfm through 80 ft of circular duct having a diameter of 28 inches. Compute the flow velocity of the air in the duct and the losses due to friction. Take the roughness of the duct to be that of medium smooth galvanized steel, $\epsilon=0.0036~\inch$.
The air velocity is found from the continuity equation:
\[v=\frac{Q}{A}=\frac{6000}{\frac{\pi}{4}(28)^2}\times 144 =~1400 ~\fpm\]The Reynolds number of the flow is
\[\Re=8.6 v D=8.6(1400)(28)=337,000\]and therefore turbulent. The relative roughness is
\[\epsilon/D=0.0036/28=0.00013\]and the friction factor $f=0.0155$ is obtained from our online calculator.
The pressure drop is then:
\[\Delta p_f=12 f \frac{L}{D}p_v=12(0.0155)\frac{80}{28}\left(\frac{1400}{4005}\right)=0.064~\inWC\]Alternatively we can use the ASHRAE friction chart.
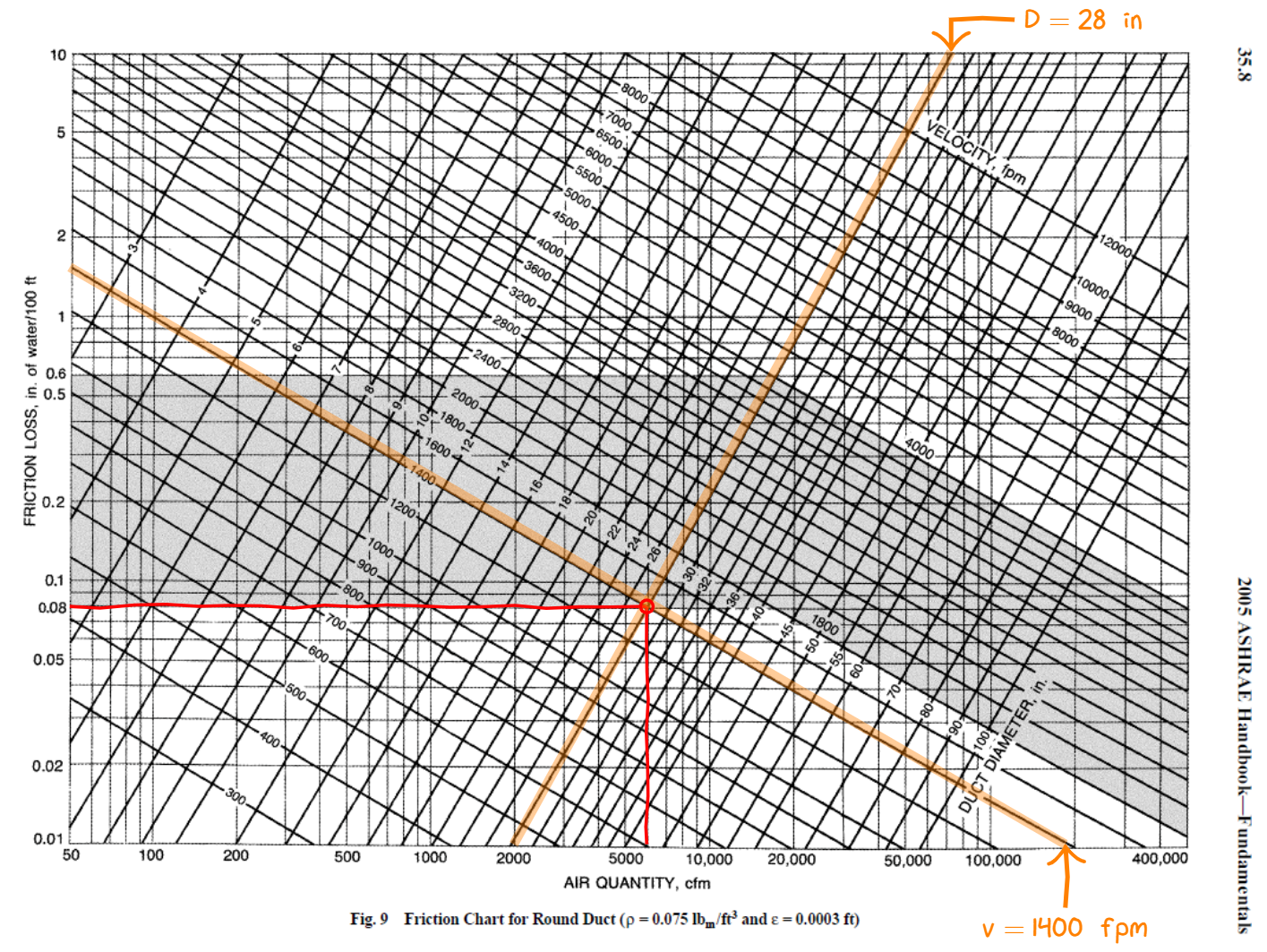
For a volume flow rate of $Q=6000~\cfm$ and duct diameter $D=28~\inch$ we find the air velcoity is $v=1400~\fpm$ and the pressure drop per 100 feet of duct is $0.08~\inWC$.
This allows us to find the friction in 100 feet of duct. In our case we have 80 feet of duct. The pressure drop is therefore
\[\Delta p_f=0.08\frac{\inWC}{100~\ft}\times 80~\ft=0.064~\inWC\]For ducts of non-circular cross section we define the equivalent diameter as
\[d_e=1.55\frac{ \mathrm{A}^{0.625} }{ \mathrm{WP}^{0.25} }\]where A is the area of the duct and WP is the wetted perimeter. Ducts that have the same $d_e$ have the same friction loss. The table Equivalent diameter of rectangular and flat oval ducts computes the equivalent diameter of rectangular ducts and flat oval ducts using the formula given above.
Find a rectangular duct and a flat oval duct that would have approximately the same friction as a circular duct of diameter 28 inches.
From the table of equivalent diameters of rectangular and flat oval ducts we find that a $22\times 30~\inch$ rectangular duct has an equivalent diameter of 28.1 inches, close enough to our circular duct of diameter 28 inches.
From the same set of tables we see that a flat oval duct with a major axis of 30 inches and a minor axis 24 inches has an equivalent diameter of 27.5 inches, close to our circular duct of diameter 28 inches. A duct having a minor axis of 26 inches would also be an acceptable choice as this has an equivalent diameter of 28.4 inches.
|
About
|
Back to Applied Fluid Mechanics Resources & Notes