Since the log is floating unsupported in the water the buoyant force equals the weight of the log. The weight of the log is $$ W=\gamma_{\rm log} V_{\rm T} $$ where $V_{\rm T}$ is the total volume of the log. The buoyant force is $$ F_b=\gamma_{\rm water} V_d $$ where $V_d$ is the displaced volume and corresponds to the volume of log that is submerged. Setting the buoyant force equal to the weight we find $$ \gamma_{\rm log} V_{\rm T}=\gamma_{\rm water} V_d $$ Solving for our unknown $$ \gamma_{\rm log} = \frac{V_d}{V_{\rm T}}\gamma_{\rm water} \label{eqa}\tag{1} $$ The next step is to solve for the two volumes. The total volume is straightforward, it is the volume of a cylinder with diameter of 450 mm. $$ V_{\rm T}=\frac{\pi}{4}\left(0.45~\m\right)^2\times 6.75~\m=1.074~\m^2 $$ The displaced volume is much more complicated. The figure below shows the cross-section of the log. The displaced volume is the length of the log times the area of part of the circle below the waterline. 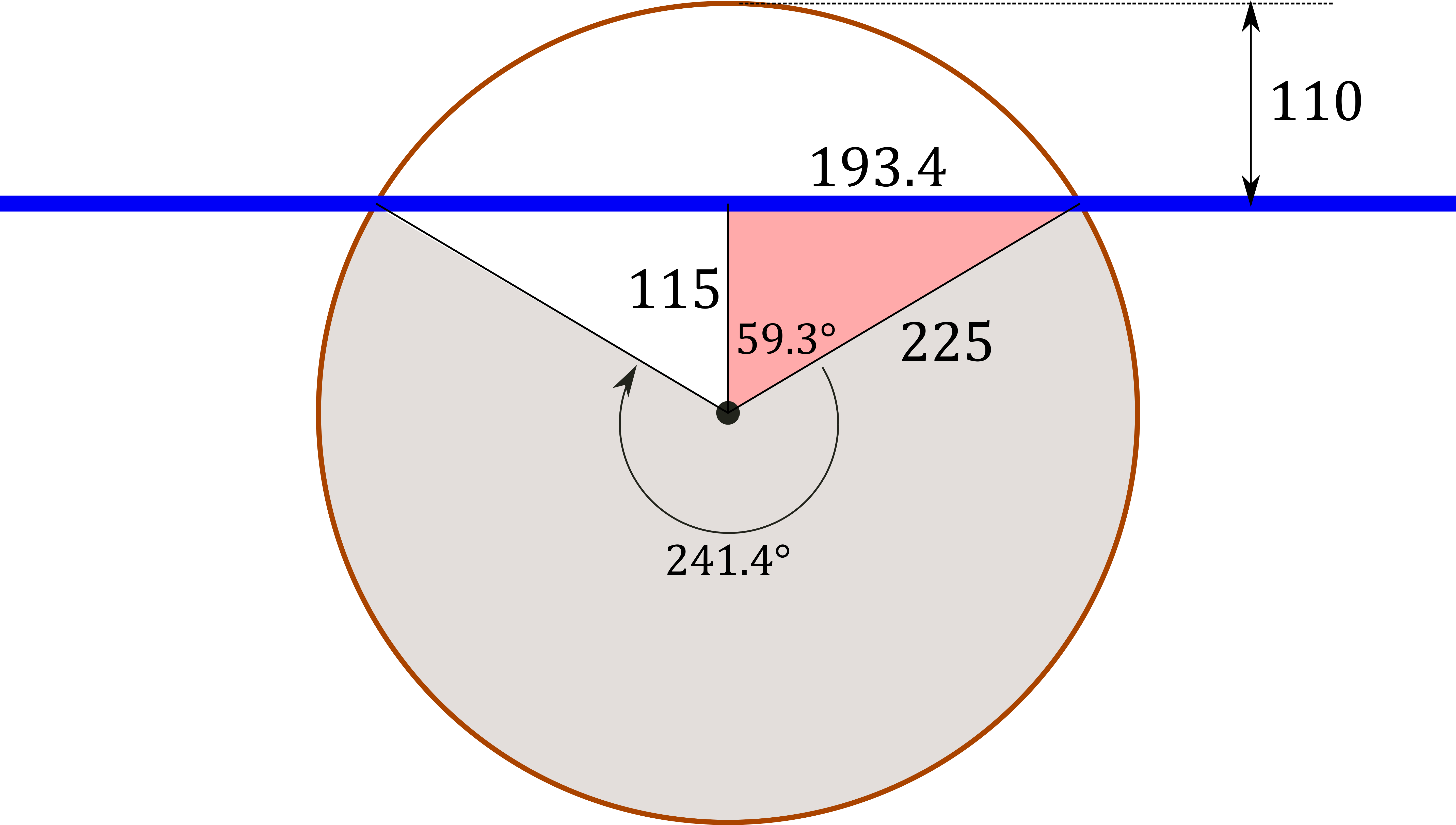To find the area we separate the region up into two triangles and a circular segment. All of the relevant dimensions are labeled in mm. The area of the shaded-pink triangle is $$ A_{⊿} = \frac{1}{2}(0.1934~\m)(0.115~\m) = 0.011~\m^2 $$ The area of the shaded-gray circular segment is $$ A_{◕}=\frac{241.4}{360}*\pi(0.225~\m)^2 = 0.107~\m^2 $$ The total displaced volume is $$ V_d=\left[ 2\times A_{⊿} + A_{◕}\right]\times 6.75~\m=\left[2\times (0.011~\m^2) + 0.107~\m^2\right]\times 6.75~\m=0.871~\m^3 $$ We now return to equation $\eqref{eqa}$ which we rewrite here: $$ \gamma_{\rm log} = \frac{V_d}{V_{\rm T}}\gamma_{\rm water} = \frac{0.871}{1.074}\left(9.81~\kN/\m^3\right)=7.95~\kN/\m^3 $$