Before we start let's first gather some data and calculate some quantities that we are likely to need. The flow velocity is $$ v=\frac{Q}{A}=\frac{20~\L/\min}{464.1\times 10^{-6} \m^2} \times \frac{1~\m^3/\s}{60,000~\L/\min} = 0.718~\m/\s $$ where the flow area was taken from my Schedule 80 Steel Pipe Data Table. Later on I'll need the inside diameter which is $$ D=24.3~\mm $$ With the expectation that we will need to compute the Reynolds number I looked up the dynamic viscosity of Benzene from NIST Chemistry WebBook. At 60°C I found that $$ \eta = 3.9419\times 10^{-4}~\Pa\cdot \s $$ The density of this Benzene is $$ \rho=\frac{\gamma}{g}=\frac{8.62 \kN/\m^2}{9.81~\m/\s^2}=879~\kg/\m^3 $$ Now we start working on the problem. The starting point is the general energy equation. Since there are no pumps or motors both $h_A$ and $h_R$ are zero. Since the pipe is horizontal $z_1=z_2$. Since the pipe has a constant cross-sectional area the velocity heads at point 1 and 2 are also equal. In this scenario the general energy equation reduces to $$ p_1 - p_2 = \gamma h_L $$ where the fluid flow is from point 1 to point 2. The energy loss due to friction is calculated from Darcy's equation $$ h_L=f \frac{L}{D} \frac{v^2}{2g} $$ In order to find the friction factor $f$ in the above expression we need to determine if the flow is laminar or turbulent. To do this we calculate the Reynolds number for the flow. $$ N_R=\frac{vD\rho}{\eta}=\frac{(0.718)(0.0243)(879)}{3.9419\times 10^{-4}}=3.89\times 10^4 $$ Since the Reynolds number is above 4000 the flow is turbulent. In order to get the friction factor we need the relative roughness of the pipe. 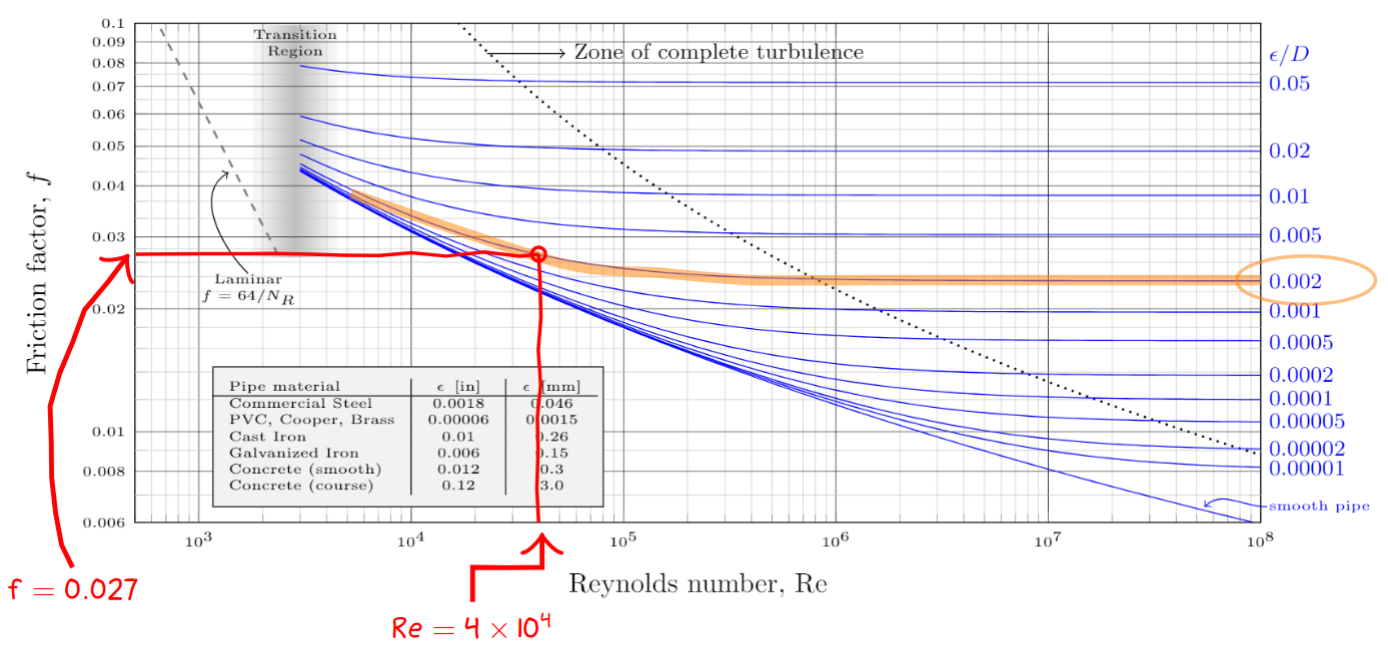For commercial steel $\epsilon=0.046~\mm$ and $$ \epsilon/D = 0.046/24.3 = 0.00189\approx 0.002 $$ The image below shows how I extracted $f=0.027$ from the Moody diagram using the curve for $\epsilon/D=0.002$ at a Reynolds number of $4\times 10^4$. This value of $f$ can be confirmed with our calculator. I can now return to Darcy's equation and evaluate the friction loss $$ h_L=f \frac{L}{D} \frac{v^2}{2g} = 0.027 \times \frac{100}{0.0243} \frac{(0.718)^2}{2 (9.81)} = 2.92~\m $$ The pressure drop is then $$ p_1 - p_2 = \gamma h_L = 8.62~\kN/\m^3 \times 2.92~\m = 25.2~\kN/\m^2 = 25.2~\kPa $$